基礎講座|精密ポンプ技術 9-5. 摩擦抵抗の計算<計算例 4・5・6>
計算例4
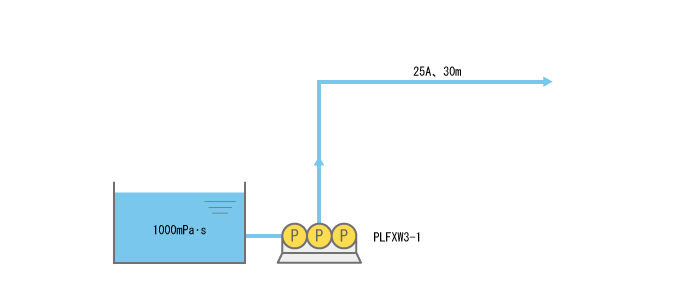
スムーズフローポンプ(3連式)PLFXW3-1を用いて、次の配管条件で注入したとき。
吐出側配管長:30m、配管径:25A = 0.025m、粘度:1000mPa・s、比重:1.0
一般に液体の粘度は温度が高いと小さく、低いと大きくなります。
手順については計算例1、2と同じです。
- «手順1» ポンプを(仮)選定する。
PLFXW3-1を選定。 - «手順2» 計算に必要な項目を整理する。(液の性質、配管条件など)
- (1) 粘度:μ = 1000mPa・s
ここで粘度1000mPa・sが問題となります。
この粘度は液温が何度の時の値かが明示されていないので、まず温度を確認することが必要です。そして温度が一定であれば、そのときの粘度を計算に用います。また温度が変化する場合は、最大と最小の粘度を調べておき、圧力損失を求める場合は最大粘度で計算します。
ここではμ = 1000mPa・sとします。 - (2) 配管径:d = 0.025m
- (3) 配管長:L = 30m
- (4) 比重量:ρ = 1000kg/m3
- (5) 吐出量:スムーズフローポンプのQaはどうなるのでしょうか。
「10-3. 摩擦抵抗の計算」の式(3)ではQa1をΠ(3.14)倍していますが、これは往復動ポンプには脈動特性があり、最大瞬間流量(ピーク流量)が平均流量のπ倍に相当することを意味しています。
ところが同じ定量ポンプであってもスムーズフローポンプにはピーク値がありませんので、平均流量のみを考えれば良いことになります。
ただし無脈動といっても3連方式では微小な脈動が残りますので「10-3. 摩擦抵抗の計算」の式(3)をΠではなく、3で割って計算してください。
(Qaは3連トータルの吐出量としてQa3と表示)
ここではQa3 = 3.6L/min(60Hz)とします。 - (6) 重力加速度:g = 9.8m/sec2
- (1)
- «手順3» 管内流速を求める。
«手順2»の(5)から流速を求める式は次のようになります。
したがって、この例の場合は
となります。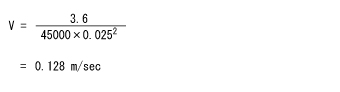
«手順4»~«手順9»は今までの例と同じです。
- «手順10» 結果の検討。
△Pの値は0.2MPaとなり、充分使用可能と判断できます。
- ※注意 「10-3. 摩擦抵抗の計算」の式(7)を用いて計算する場合も、Qaを3で割った後で必要項目を代入してください。
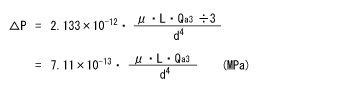
△P:管内の摩擦抵抗による圧力損失(MPa)
μ:粘度(mPa・s)
L:配管長さ(m)
Qa3:3連トータルの平均流量(L/min)
d:配管内径(m)
計算例5
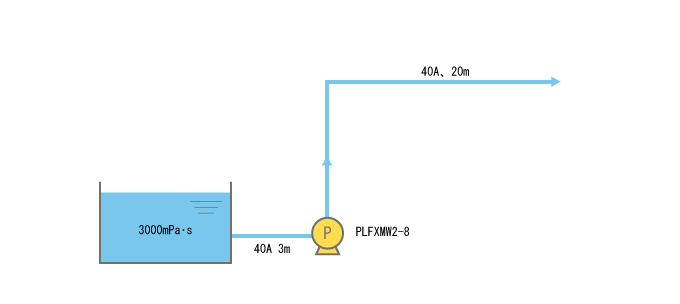
スムーズフローポンプ(2連式)PLFXMW2-8を用いて、次の配管条件で注入したとき。
吐出側配管長:20m、吸込側配管長:3m、配管径:40A = 0.04m、粘度:3000mPa・s(20℃)、比重:1.0
手順については計算例1、2と同じです。
- «手順1» ポンプを(仮)選定する。
PLFXMW2-8を選定。 - «手順2» 計算に必要な項目を整理する。(液の性質、配管条件など)
- (1) 粘度:μ = 3000mPa・s
- (2) 配管径:d = 0.04m
- (3) 配管長:
吐出側L1 = 20m
吸込側L2 = 3m - (4) 比重量:ρ = 1000kg/m3
- (5) 吐出量:Qa2 = 16L/min(60Hz)
スムーズフローポンプ(2連式)の吐出量はQa2と表します。つまり2連トータルの吐出量です。 - (6) 重力加速度:g = 9.8m/sec2
- (1)
- «手順3» 管内流速を求める。
計算例4はスムーズフローポンプ(3連式)の場合でしたが、ここではスムーズフローポンプ(2連式)を使用しています。なぜこの«計算例5»では、特に吸込側の配管条件を明記しているのでしょうか。
ここに3連式と2連式との大きな違いがあります。- (1) スムーズフローポンプ(3連式)は、吐出側、吸込側ともに無脈動になります。
- (2)
つまり流速は次の式
で求められます。この例では、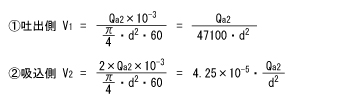
となります。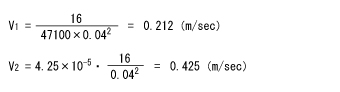
- (1)
«手順4»~«手順9»は今までの例と同じです。
- «手順10» 結果の検討。
△Pの値を計算すると、吐出側は0.254MPaとなり使用可能のようですが、吸込側は0.076MPaで許容限界を超えてしまっています。
したがって配管の内径を太くして圧力損失を0.05MPa以内にしなければなりません。
ここで式(7)を変形します。
この式は脈動によるピーク流量を考慮して、平均流量が既にΠ倍されています。またスムーズフローポンプ(2連式)の吸込側では、上記のように1連の場合の2倍相当の流れになります。したがって△Pを求めるには、式(7)を一旦Πで割って1連ポンプの脈動の影響を相殺し、次に新たに2をかけて求めることができます。
が導かれます。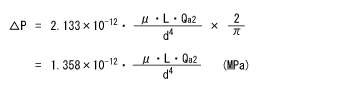
«この式にはμをmPa・s単位で、Lはm単位で代入します»
この式でd = 0.05のときの△Pの値は0.031MPaになり、使用可能範囲内まで低下します。したがって吸込側の配管には50Aを用いれば良いことが判ります。
このようにスムーズフローポンプ(2連式)を使用する場合は、特に吸込側配管に注意してください。
計算例6
モータ駆動定量ポンプFXD2-10Pを用いて、次の配管条件で注入したとき。
吐出側配管長:20m、配管径:40A = 0.04m、粘度:500mPa・s(20℃)、比重:1.0
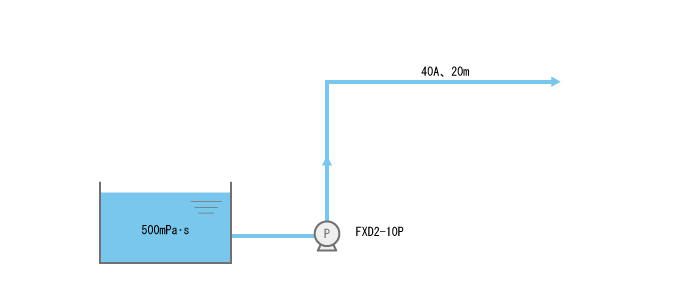
手順については計算例1、2と同じです。
- «手順1» ポンプを(仮)選定する。
FXD2-10Pを選定。 - «手順2» 計算に必要な項目を整理する。(液の性質、配管条件など)
- (1) 粘度:μ = 500mPa・s
- (2) 配管径:d = 0.04m
- (3) 吐出側配管長:L = 20m
- (4) 比重量:ρ = 1000kg/m3
- (5) 吐出量:
このポンプの最大吐出量は24L/minですが、この数値をそのままQaに代入する訳にはいきません。というのは、このポンプの左右のストロークの位相が180°ずれているからです。つまり、片方のポンプ(2連のうちの1連)が液を押し出しているとき、もう一方は液を吸い込んでいるために液を吐出していないということです。したがって圧力損失を求める際には、1連分の吐出量で計算すれば良いことになります。
ここでは、Qa1 = 24 ÷ 2 = 12L/min(60Hz)として計算します。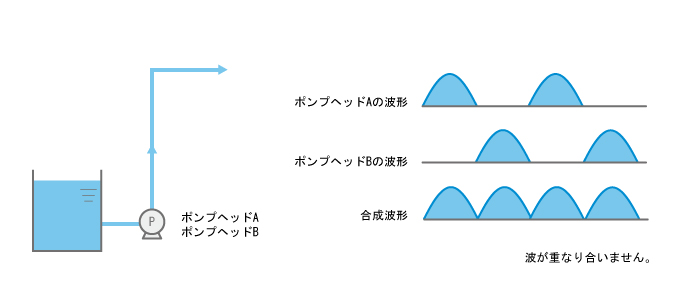
- (6) 重力加速度:g = 9.8m/sec2
- (1)
«手順3»~«手順9»は今までの例と同じです。
- «手順10» 結果の検討。
△Pは約0.1MPaとなり、摩擦抵抗に関しては問題ありません。
この例で、ポンプの吐出側にエアチャンバーを設置するとどうなるでしょうか。
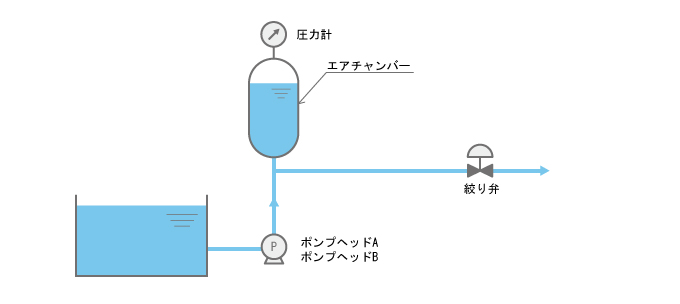
エアチャンバーを定量ポンプに使用する目的は、脈動を極力なくして圧力損失を低減させたり、配管などの振動を防止したりすることです。
この場合の流量(Qa)は2連分が連続して流れますので、24L/minになります。ただし「10-3. 摩擦抵抗の計算」の(3)式でQa1をΠ(3.14)倍する必要はありません。
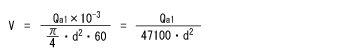
が流速を求める式になります。
ちなみに△Pは0.064MPaが得られます。
ただしエアチャンバーを用いる方法では、完全に脈動を消すことはできません。2割程度余裕をとって△Pを0.08MPaくらいに考えた方が良いでしょう。


